Problema del OR Exclusivo
Una de las principales razones por la que las redes neuronales desaparecieron de la mayoría de los proyectos de investigación durante la década de los 70 y parte de los 80 fue que las redes conocidas hasta entonces, cuyo exponente máximo era el perceptrón (hoy en día perceptrón simple); no eran capaces de solucionar problemas no linealmente separables.
Para problemas linealmente separables, existían soluciones algorítmicas tradicionales eficientes, luego no tenía sentido utilizar la tecnología neuronal.
Para que nos hagamos una idea, un problema linealmente separable es aquél que puede dividirse en dos áreas claramente diferenciadas mediante una línea. Vale cualquier línea para separarlos, tan compleja como se desee.
Por ejemplo, si el problema que queremos resolver es saber dadas dos entradas, cuál es el resultado de realizar la operación lógica OR entre ellas, podemos dividir el problema linealmente de forma sencilla:
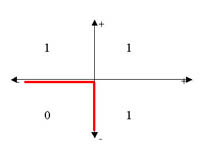
Sin embargo, si lo que quisiéramos es calcular el OR exclusivo de las entradas, no podemos separar linealmente el problema:
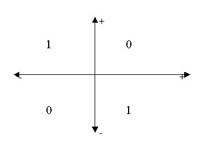
Esta operación tan sencilla marca ya una barrera en las redes neuronales, que no se romperá hasta que en 1986 Rumelhart y McClelland diseñaran el perceptrón multicapa (o MLP, multilayer perceptron), revolucionando todo lo conocido hasta entonces en redes neuronales.
El siguiente applet realiza mediante un perceptrón multicapa esta operación de OR Exclusivo. Aunque no es un ejemplo demasiado bueno de la potencia que podemos alcanzar con los MLP, sí que nos permite ver varias características básicas del mismo: curva de aprendizaje, resolución de problemas no linealmente separables, tipos de aprendizaje, error y aproximaciones, etc.
ARQUITECTURA
La arquitectura de este applet consta de 3 capas, cada una totalmente conectada con la siguiente:
-
Capa de Entrada de dos neuronas, que tomará los dos valores para hacer la operación. Aunque estos valores son binarios, la red está programada de forma que podría aceptar valores continuos y dar la respuesta adecuada.
-
Capa Oculta, con un número configurable de neuronas mediante la opción nº de neuronas ocultas. El hecho de que exista la capa oculta es la que da al perceptrón multicapa la capacidad de resolver problemas no separables linealmente. La cantidad de neuronas que se utilicen hace que varíe el tiempo que se tarda en minimizar el error. 1 neurona hace el trabajo muy lento, 2 ó 3 son el número más adecuado (de 6000 a 40000 iteraciones para un error de 0.1). 4 ó más son muy eficientes (menos de 15000 its.), pero aumentan la carga de trabajo en cada iteración al aumentar el número de pesos a calcular.
-
Capa de salida. Una sola neurona que nos da el valor del XOR entre las dos entradas. Se ha mantenido un valor continuo de salida para que pueda observarse el efecto de tolerar más o menos error.
El botón cargar red nos permite crear una red ya entrenada con un error muy bajo, para comprobar la máxima eficiencia del perceptrón sin necesidad de entrenar la red.
ENTRENAMIENTO
Durante el entrenamiento, mostramos a la red el juego de ensayo, que es la tabla del XOR:
|
A |
B |
XOR |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
El entrenamiento se realiza con retropropagación batch (se pasan los cuatro juego de ensayo antes de modificar los pesos). En el gráfico podemos observar el descenso del error cuadrático medio según aumentan las iteraciones.
Podemos configurar:
- Momento: controla en qué grado el estado en el que se encuentra la red neuronal influye en el estado que tendrá en el siguiente paso del aprendizaje.
- Factor de Aprendizaje: controla el efecto del error en la modificación de los pesos de las capas de neuronas.
- Nº de Iteraciones: número máximo de iteraciones que usaremos para entrenar la red. Si no se alcanza el error máximo tolerado en esas iteraciones, la red trabajará con el error al que haya llegado.
- Error Máximo: error cuadrático medio (MSE, Medium Square Error) máximo que tolerará la red. Mientras no se haya alcanzado, continuará el entrenamiento hasta que se alcance, o hasta que agotemos las iteraciones estipuladas, lo que ocurra primero. Se observa claramente que el error máximo influye en la respuesta de la red. Con un error de 0.1, la red responde a una entrada 0,0 con un 0.15, mientras que si el error es de 0.01 nos da un 0.08. Mediante el botón Cargar Red podemos usar unos pesos entrenados para un error de 0.01 para una red de 3 neuronas ocultas.