Compresión de Imágenes
Un problema que se ha abordado de muy distintas formas en la informática, y sobre todo desde el auge de Internet, es la compresión de ficheros de cualquier tipo.
La compresión de ficheros mediante redes neuronales difiere un poco de otros tipos de compresión. La mayoría de compresiones se basan en un algoritmo de compresión que aproveche características conocidas, elimine información redundante, etc; para luego poderlo reconstruir a partir de esas mismas premisas.
La compresión mediante MLP es bastante más abstracta. Se basa de alguna forma en la capacidad de almacenamiento del cerebro, que abstrae patrones de la información, pudiendo después reconstruir la información al completo.
La compresión en sí no se basa en ningún algoritmo, si no que usamos una arquitectura de "cuello de botella" para nuestro perceptrón. Usaremos este método para comprimir imágenes 128x128 en blanco y negro.
ARQUITECTURA
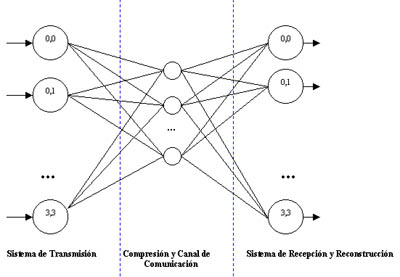
La capa de entrada representa el conjunto de píxeles que forman la imagen. Usamos 16 neuronas de entrada, con lo que sólo podemos pasar imágenes 4x4. La imagen original 128x128 se "troceará" en 1024 imágenes 4x4.
La capa oculta es la que da el nombre de red de cuello de botella, pues tendrá un número reducido de neuronas, menor o igual a las 16 neuronas de entrada. Representaría en un canal de comunicación tanto la compresión como la transmisión de la imagen. El número de neuronas nos da el grado de la compresión (menos neuronas ocultas, mayor compresión).
Por ejemplo, si usamos 16 neuronas ocultas, no tendremos compresión. Aún así puede servir para investigar el comportamiento frente al "ruido" que representa la propia inexactitud de los pesos, que se puede equiparar al ruido del canal. 8 neuronas ocultas serán un 50% de reducción en la imagen, del mismo modo que 4 serán un 75%, etc.
La capa de salida tiene tantas neuronas como la de entrada (16) y se correspondería con el terminal de recepción y reconstrucción de la imagen.
Todo el proceso se puede ver más claro con este dibujo:
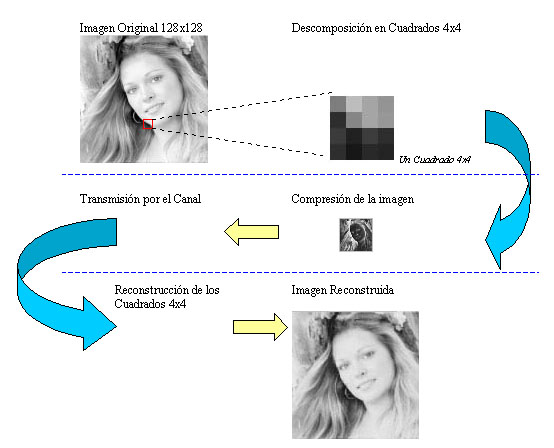
ENTRENAMIENTO
Para entrenar la red, seleccionamos 256 cuadrados 4x4 de una cierta imagen. Los cuadrados son trozos de posiciones aleatorias de la imagen. Estos cuadrados forman el juego de entrenamiento, que se mostrará a la red durante un cierto número de iteraciones.
Puede verse claramente que el tamaño del juego de ensayo es bastante grande si lo comparamos con el ejemplo del XOR, así que el entrenamiento (sobre todo si queremos errores menores que 1.0) puede llevar bastante tiempo. La curva de aprendizaje tiene un aspecto similar a éste, asintótica en y=0 y x=0:
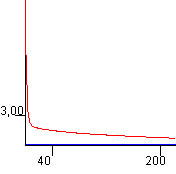
Ya que el entrenamiento puede resultar tedioso, y aprovechando las propiedades de la congelación de pesos una vez entrenada la red, se ha incluido el botón Cargar Pesos que nos da una red ya entrenada en un error bajo; con el que podemos ver los resultados mejores que hemos conseguido con la red.
Éste es también un buen ejemplo para comprobar la capacidad de generalización de las redes neuronales. Sin que importe qué imagen hemos usado para entrenar, cualquier otra imagen que comprimamos una vez entrenada la red será descomprimida con la misma precisión. Incluso imágenes a color (como art.jpg), son descomprimidas perfectamente, pero en blanco y negro. Tampoco tiene problemas con imágenes de una tamaño mayor o menor a 128x128