Solución sencilla de una ecuación de tercer grado

1. Solución

Vamos a solucionar la ecuación de tercer grado: $x^{3} - 621 x^{2} + 96720 x - 1154608 = 0$

Eliminamos primero el coeficiente del término de segundo grado haciendo el cambio de variables $y = x - x_{0}$ :

{(y + x_{0})}^{3} - 621 {(y + x_{0})}^{2} + 96720 (y + x_{0}) - 1154608 = 0

y^{3} + (3 x_{0} - 621) y^{2} + (3 x_{0}^{2} - 1242 x_{0} + 96720) y + (x_{0}^{3} - 621 x_{0}^{2} + 96720 x_{0} - 1154608) = 0

Elegimos $x_{0}$ de modo que se anule el coeficiente de $y^{2}$ :

3 x_{0} - 621 = 0 \Rightarrow x_{0} = 207

El cambio de variables que hacemos es $y = x - 207$ y la ecuación resultante en y, sustituyendo $x_{0} = 207$ , es:

y^{3} - 31827 y + 1126946 = 0

Si llamamos $y_{1}$ , $y_{2}$ y $y_{3}$ a las soluciones de la ecuación anterior, se ha de verificar que:

y^{3} - 31827 y + 1126946 = 0 = (y - y_{1}) (y - y_{2}) (y - y_{3}) =

y^{3} - (y_{1} + y_{2} + y_{3}) y^{2} + (y_{1} y_{2} + y_{2} y_{3} + y_{3} y_{1}) y - y_{1} y_{2} y_{3}

De ello, se deduce, igualando los coeficientes de los términos en $y$ :

$y_{1} + y_{2} + y_{3}$	$=$	$0$	[1]
$y_{1} y_{2} + y_{2} y_{3} + y_{3} y_{1}$	$=$	$- 31827$	[2]
$y_{1} y_{2} y_{3}$	$=$	$- 1126946$	[3]

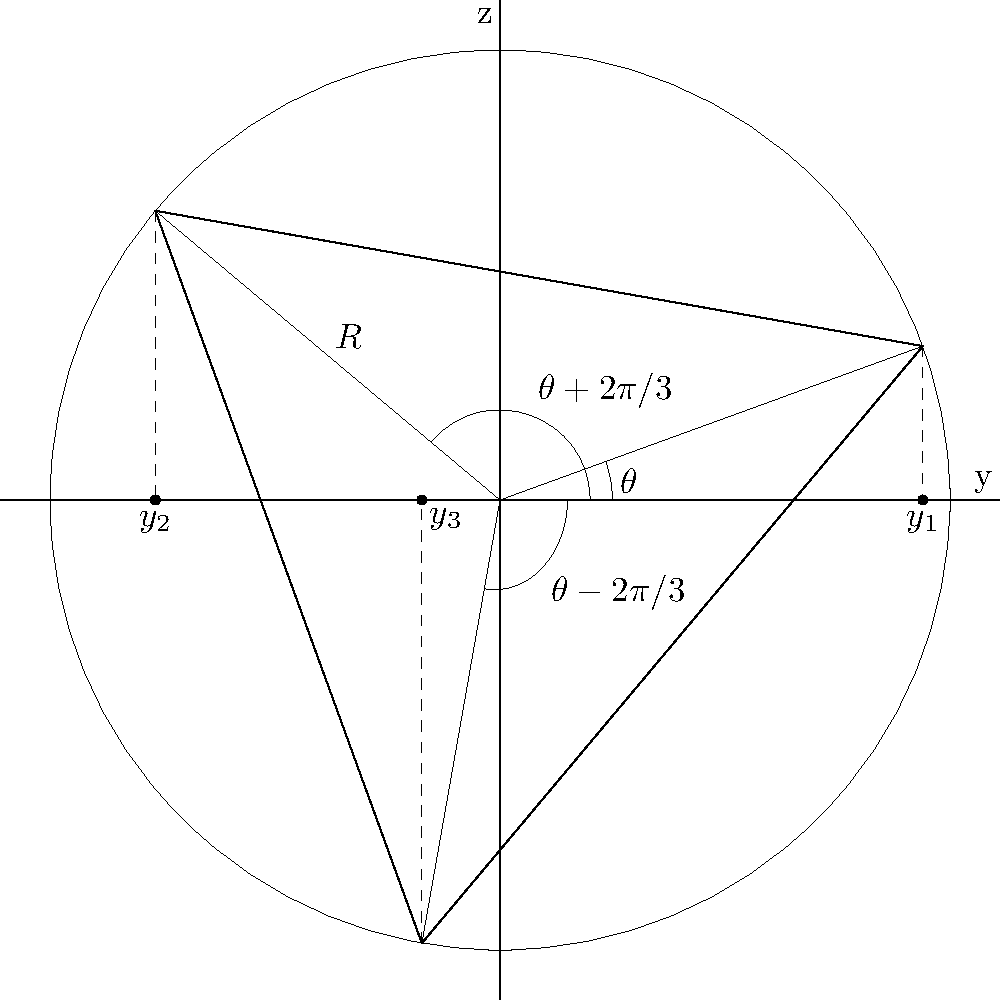
Tomemos como soluciones de la ecuación las proyecciones sobre el eje $y$ de los tres vértices de un triángulo equilátero girado inscrito en una circunferencia de radio $R$ :

$y_{1}$	$=$	$R ⋅ cos θ$			[4]
$y_{2}$	$=$	$R ⋅ cos (θ + \frac{2 π}{3})$	$=$	$−R ⋅ \frac{\cos θ + \sqrt{3} \sin θ}{2}$	[5]
$y_{3}$	$=$	$R ⋅ cos (θ - \frac{2 π}{3})$	$=$	$−R ⋅ \frac{\cos θ - \sqrt{3} \sin θ}{2}$	[6]

Sustituyendo [4], [5] y [6] en [1], [2] y [3], respectivamente:

$y_{1} + y_{2} + y_{3}$	$=$	$0$	$=$	$0$	[7]
$y_{1} y_{2} + y_{2} y_{3} + y_{3} y_{1}$	$=$	$- \frac{3 R^{2}}{4}$	$=$	$- 31827$	[8]
$y_{1} y_{2} y_{3}$	$=$	$R^{3} \cdot \frac{4 \cos^{3} θ - 3 \cos θ}{4}$	$=$	$- 1126946$	[9]

Podemos calular $R$ inmediatamente a partir de [8]:

R = \sqrt{\frac{4 \cdot 31827}{3}} = 206

De esto último deducimos que las raíces de la ecuación en $y$ están en el intervalo [-206,206]. Para calcularlas explícitamente nos basamos en [9] y en la identidad:

\cos (3 θ) = 4 \cos^{3} θ - 3 \cos θ

Y, por tanto:

y_{1} y_{2} y_{3} = R^{3} \cdot \frac{4 \cos^{3} θ - 3 \cos θ}{4} = R^{3} \cdot \frac{\cos (3 θ)}{4} = - 1126946

Despejamos el coseno y sustituimos el valor de $R$ :

\cos (3 θ) = - \frac{4 \cdot 1126946}{206^{3}} = - 0,515657616

3 θ = \arccos (- 0,515657616) = 2,112571329

θ = \frac{2,112571329}{3} = 0,704190443

Y las soluciones de la ecuación en $y$ son:

$y_{1}$	$=$	$206 ⋅cos 0,704190443$	$=$	$157$
$y_{2}$	$=$	$206 ⋅cos (0,704190443 + \frac{2 π}{3})$	$=$	$- 194$
$y_{3}$	$=$	$206 ⋅cos (0,704190443 - \frac{2 π}{3})$	$=$	$37$

Deshacemos el cambio de variable para encontrar nuestras flamantes soluciones:

$x_{1}$	$=$	$y_{1} + 207$	$=$	$364$
$x_{2}$	$=$	$y_{2} + 207$	$=$	$13$
$x_{3}$	$=$	$y_{3} + 207$	$=$	$244$

No queda más que sustituir para verificar...

$x_{1}^{3} - 621 x_{1}^{2} + 96720 x_{1} - 1154608$	$=$	$364^{3} - 621 \cdot 364^{2} + 96720 \cdot 364 - 1154608$	$=$	$0$
$x_{2}^{3} - 621 x_{2}^{2} + 96720 x_{2} - 1154608$	$=$	$13^{3} - 621 \cdot 13^{2} + 96720 \cdot 13 - 1154608$	$=$	$0$
$x_{3}^{3} - 621 x_{3}^{2} + 96720 x_{3} - 1154608$	$=$	$244^{3} - 621 \cdot 244^{2} + 96720 \cdot 244 - 1154608$	$=$	$0$

2. Observaciones

¡Un momento! La raíz cuadrada también puede ser negativa:

R = - \sqrt{\frac{4 \cdot 31827}{3}} = - 206

\cos (3 θ) = - \frac{4 \cdot 1126946}{{(- 206)}^{3}} = 0,515657616

3 θ = \arccos (0,515657616) = 1,029021324

θ = \frac{1,029021324}{3} = 0,343007108

La solución para las $y$ queda ahora:

$y_{1}$	$=$	$- 206 ⋅cos 0,343007108$	$=$	$- 194$
$y_{2}$	$=$	$- 206 ⋅cos (0,343007108 + \frac{2 π}{3})$	$=$	$157$
$y_{3}$	$=$	$- 206 ⋅cos (0,343007108 - \frac{2 π}{3})$	$=$	$37$

Y para $x$ :

$x_{1}$	$=$	$y_{1} + 207$	$=$	$13$
$x_{2}$	$=$	$y_{2} + 207$	$=$	$364$
$x_{3}$	$=$	$y_{3} + 207$	$=$	$244$

Son las mismas soluciones, pero en otro orden.

¿Qué hubiera pasado si $R^{2}$ fuera negativo? Pues que $\cos (3 θ)$ sería imaginario puro.

¿Y si $| \cos (3 θ) |$ fuera mayor que la unidad?

La respuesta está en el coseno de un número complejo:

\cos (a + ib) = \cos a \cdot \cosh b - i \sin a \cdot \sinh b

Si el módulo del coseno es real y mayor que la unidad, el ángulo es imaginario puro. Si el coseno es imaginario puro, el ángulo es complejo y su parte real es $\pm \frac{π}{2}$ .

3. Ejemplo con números complejos arbitrarios

Resolvamos: $x^{3} + (12 + 23 i) x - (47 - i) = 0$

Calculamos el radio:

R = \sqrt{- \frac{4 \cdot (12 + 23 i)}{3}} = 3,0487422042700056 + 5,0293964874622015 i

Ahora el ángulo:

\cos (3 θ) = - \frac{4 (47 - i)}{{(- 3,0487422042700056 + 5,0293964874622015 i)}^{3}} = - 0,9235043359285389 - 0,039544454953160564 i

θ = \frac{\arccos (- 0,9235043359285389 - 0,039544454953160564 i)}{3} = 0,9120257325875425 + 0,033358074173984446 i

Y las soluciones:

$x_{1}$	$=$	$(3,0487422042700056 + 5,0293964874622015 i) ⋅cos (- 0,9120257325875425 - 0,033358074173984446 i)$	$=$	$2 + 3 i$
$x_{2}$	$=$	$(3,0487422042700056 + 5,0293964874622015 i) ⋅cos (- 0,9120257325875425 - 0,033358074173984446 i + \frac{2 π}{3})$	$=$	$1 + 2 i$
$x_{3}$	$=$	$(3,0487422042700056 + 5,0293964874622015 i) ⋅cos (- 0,9120257325875425 - 0,033358074173984446 i - \frac{2 π}{3})$	$=$	$- 3 - 5 i$

que son las tres soluciones de la ecuación de arriba.