Números aleatorios
Un ordenador es realmente lo menos parecido a un ser impredecible. Al tratarse de un autómata, su comportamiento futuro viene marcado por las entradas y su estado anterior. Por eso, un ordenador encuentra difícil el hacer cosas al azar, como puede ser ofrecernos un número aleatorio.Lo más que puede hacer es, mediante algún truco matemático, proporcionarnos números que parezcan al azar, aunque no lo sean. Una posibilidad es usar la siguiente fórmula:
Es evidente que al usar una fórmula matemática siempre nos va a dar la misma serie de números. Lo que podemos hacer es disimularlo empezando, cada vez, en un sitio diferente, es decir, usando como número de partida uno diferente en cada ocasión. A ese número se le denomina semilla del generador. Veamos cuál es la serie que se produce si usamos como semilla el número 27:
Parecen bastante al azar, ¿o no?
Ejercicio
Cread una biblioteca que se llamerand.lib y que proporcione
estas dos funciones:
srand: se le pasa en el registro D la semilla inicial del generador de números aleatorios definido en el apartado anteriorrand: devuelve en D el siguiente número aleatorio generado
Usad la biblioteca para hacer un pequeño programa que simule
un sorteo de la Lotería Primitiva: se le introduce la fecha
de hoy como un número entero con el formato mmdd y el programa
nos da el resultado del sorteo. Si el día es el 15 de agosto,
por ejemplo, se ha de introducir 0815.
Pista: el número de la fecha se utiliza como semilla del generador. Para obtener los números del sorteo, se pide un número aleatorio al generador y nos quedamos con los 6 últimos bits. Esto nos da un número al azar del 0 al 63. Si es el 0 o es mayor que 49 o ya ha salido, pedimos otro. Si no, lo imprimimos. Así seis veces y una más para el número complementario.
El resultado del sorteo para el 15 de agosto sale, en este orden:
45, 42, 48, 25, 6 y 7. Complementario: 44.
Punteros
Los registros índices X e Y, así como los registros U y S, cuando los hacemos funcionar como índices, están pensados para contener una dirección de memoria. Hay modos en el ensamblador del 6809 de actuar sobre la dirección de memoria a la que apuntan estos registros (incluso con un desplazamiento o con autoincremento o autodecremento, como hemos visto).Puede ocurrir que, en determinadas circunstancias, nos quedemos cortos de registros índices y tengamos que usar una variable almacenada en la memoria (que será una palabra, 16 bits) para ese propósito. Se trata de un puntero.
Imaginemos que tenemos una de esas variables y queremos cargar A con
el contenido de la dirección a la que apunta el puntero p.
Podemos hacerlo del siguiente modo:
p: .word 0x400 ; direcciOn a la que apunta el puntero
[...]
ldx p ; X tiene ahora 0x400
lda ,x ; A tiene el contenido de la dirección apuntada por p
Pero esto nos ensucia el registro X. Hay una manera de hacerlo directamente en el ensamblador del 6809:
p: .word 0x400 ; direcciOn a la que apunta el puntero
[...]
lda [p] ; A tiene el contenido de la dirección apuntada por p
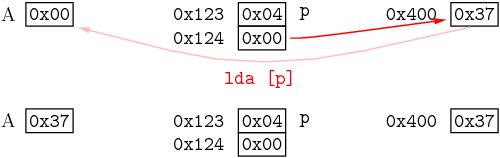
El esquema es totalmente transladable y compatible en la mayoría de casos en que, además, se usa un registro índice: cada vez que el operando esté rodeado por un par de corchetes significa que, una vez alcanzada la dirección expresada por el interior de los corchetes, hay que dar un paso más para obtener el dato. En ese lugar hay un puntero que apunta al dato:
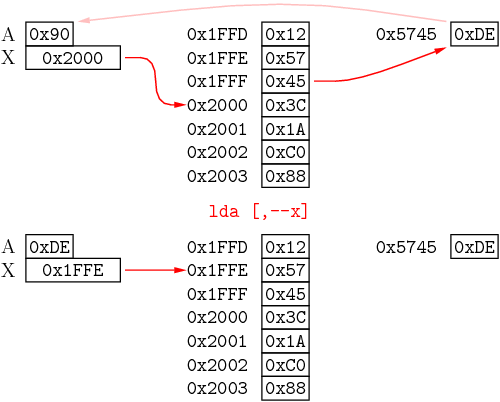
La instrucción de la figura anterior ocurre del siguiente modo: al tratarse de un predecremento, primero se decrementa X en dos unidades. Como es acceso entre corchetes, se obtiene el puntero almacenado en la dirección de memoria apuntada por X (0x1FFE): 0x5745. Se acude a esa dirección de memoria, se toma el valor allí almacenado y se carga en A.
Cuando aparecen registros índice en casos como este, es común que se trate de tablas de punteros.
Modos de direccionamiento
Cuando una orden del código máquina necesita argumentos, especialmente si estos se encuentran en la memoria, al procedimiento que se usa para obtenerlos se denomina modo de direccionamiento.En general, en el 6809, las operaciones direccionarán, como máximo un argumento, pues aquellas operaciones que requieren dos, como la suma, siempre obtienen el primero de ellos del acumulador y direccionan solamente el segundo.
Hemos visto ya algunos modos de direccionamiento. Es hora de ser un poco más sistemáticos y que conozcamos el nombren que reciben en el ensamblador del 6809:
- Inherente: la referencia al argumento se encuentra en el propio operador. Por ejemplo, CLRA
- Inmediato: el argumento es un valor numérico que se especifica directamente. Por ejemplo, LDA #7
- Extendido: en otros procesadores se denomina directo. En este hay un modo directo diferente, por eso este se llama extendido. El dato se encuentra en la dirección de memoria que se especifica. Por ejemplo, LDA 0x400
- Indizado: a veces también se le llama indexado. Para conseguir el dato, nos apoyamos en un registro índice y puede haber un desplazamiento sobre él. Por ejemplo: LDA 7,X
- Indirecto: se especifica una dirección de memoria donde se encuentra un puntero que apunta al dato. Por ejemplo: LDA [0x888]
- Indizado indirecto: acceso indizado a un puntero que señala donde se encuentra el dato. Por ejemplo, LDA [-4,Y]
La lista no acaba ahí y aún nos queda por conocer un par de modos de direccionamiento adicionales.
El modo indizado admite cuatro subvariedades siempre que el desplazamiento sea cero: predecremento doble, predecremento, postincremento y postincremento doble. Actúan sobre el registro índice usado, como ya hemos visto. El modo indizado indirecto admite, también cuando el desplazamiento es cero, solamente dos subvariedades: predecremento doble y postincremento doble. La razón de la ausencia de los otros dos es que, al tratarse de punteros y, por ello, valores de 16 bits, tiene poco sentido decrementar o incrementar el índice un byte solo.
Para acabar, el desplazamiento de un modo indizado o indizado indirecto puede también ser el registro A, B o D (todos considerados con signo).
Dirección efectiva:
Al existir tantos y tan variados modos de direccionamiento, a veces resulta un dolor de cabeza el saber dónde, en un determinado acceso, vamos a acabar tomando o depositando el dato. Esa dirección que resulta después de haber hecho todas las operaciones de direccionamiento se denomina en el 6809 dirección efectiva. Así, en el caso de la última figura, donde se explicaba la instrucción LDA [,--X], la dirección efectiva era 0x5745, pues de ahí se extraía finalmente el dato.El 6809 dispone de una instrucción para cargar en un registro la dirección efectiva de un acceso a memoria. Su nombre es LEA (Load Effective Address) y permite cargar dicha dirección en cualquiera de los registros X, Y, S o U. Veamos un ejemplo de su funcionamiento:
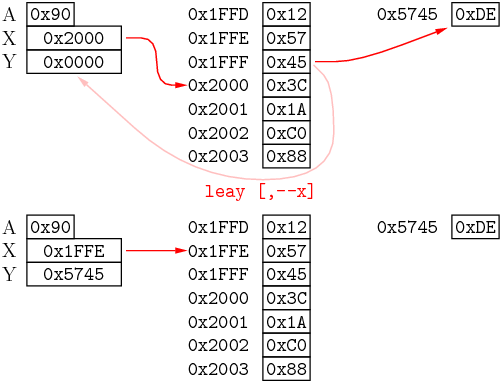
A la postre, y no es seguro de que se tratara de un objetivo premeditado, la instrucción LEA resultó también ser bastante útil para efectuar aritmética sencilla con los registros X, Y, S y U. Valgan como ejemplo estas posibilidades:
- Incrementar el registro X: LEAX 1,X
- Decrementar el registro Y: LEAY -1,Y
- Hacer que U contenga D+X: LEAU D,X
- Incrementar en una unidad X y copiar el resultado en Y: LEAY 1,X
- Despreciar el byte superior de la pila S (sacarlo y no almacenarlo en ningún sitio): LEAS 1,S
Ejercicio
Apoyándonos en la bibliotecarand del primer
ejercicio, se pide al usuario un número. Dicho número se
usará como semilla inicial. Además, se obtendrán tantos
números aleatorios como indique el número introducido y se
irán imprimiendo en la pantalla.
A continuación, se imprimirá de nuevo la lista de números, pero ordenados de menor a mayor.
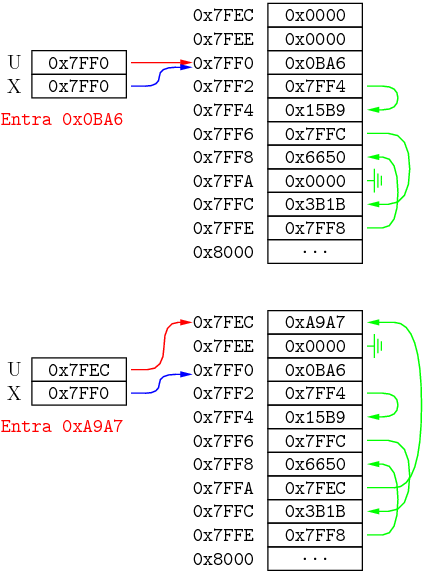
Para conseguir esto, los número se irán almacenando, ordenados, en una lista enlazada. El registro X apunta a la cabeza de la lista y el registro U servirá para construir una pila de donde se obtiene la memoria para los nodos de la lista.
Cada celda estará formada por dos palabras. La primera contiene su número aleatorio y la segunda un puntero que señala a la siguiente celda o que es cero si es la última celda.
Al llegar un número nuevo, se obtiene memoria de la pila, y se recorre la lista hasta almacenarlo en la posición que le corresponda.
Al final, se recorre la lista y se imprimen los números, que estarán ordenados.
Este es el resultado para el caso de que se introduzca el número 10:
15131 26192 5561 2982 43431 1420 45669 36226 8051 24840 1420 2982 5561 8051 15131 24840 26192 36226 43431 45669
Y así se dispone la lista enlazada para este ejemplo en los primeros números, que en hexadecimal son: 0x3B1B, 0x6650, 0x15B9, 0x0BA6, 0xA9A7, 0x058C, 0xB265, 0x8D82, 0x1F73 y 0x6108.
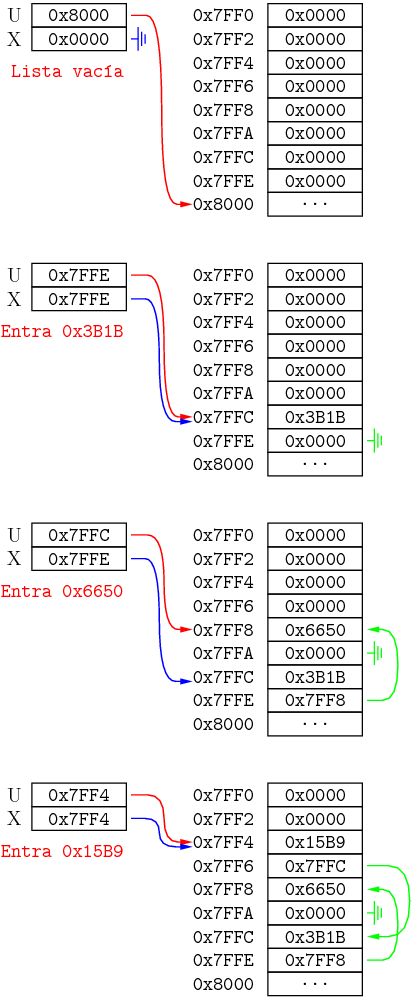
Un par de casos más para llegar a uno que se pone al final de la lista...
Tablas de salto
Las operaciones JMP y JSR permiten elegir la dirección a la que se quiere saltar de modo directo como hemos visto, pero también de modo indizado o indirecto. En general, podemos decir que JMP sería equivalente a una instrucción que se denominara LEAPC y JSR, lo mismo respecto al objetivo del salto, pero haciendo las operaciones propias de un salto a una subrutina.Estas operaciones se usan frecuentemente con esos tipos de direccionamiento cuando se quieren programar tablas de salto. Estas tablas son tablas cuyos elementos son direcciones de subrutinas. Se selecciona a qué subrutina saltar simplemente con un desplazamiento en la tabla.

Si el número de subrutinas es grande y no es fija la rutina a la que se debe saltar sino que su desplazamiento está contenido en un registro, las tablas de salto son una herramienta poderosa para ganar tiempo. La alternativa consistiría en ir comparando el contenido del registro con 0, 1, 2, 3, etc. hasta acertar y saltar a la rutina que corresponda:
;; el nUmero de la rutina estA en A
tsta
bne b1
jsr subrutina0
bra seguir
b1: cmpa #1
bne b2
jsr subrutina1
bra seguir
b2: cmpa #2
bne b3
jsr subrutina2
bra seguir
[...]
Ejercicio
Pedid dos números de dos cifras al usuario. Presentad a continuación un menú con tres opciones: sumarlos, restarlos o multiplicarlos. Que el usuario pulse 1, 2 ó 3, según la opción que prefiera. Confeccionad, mediante una tabla de salto, el salto a una subrutina que realice la operación elegida y presentad el resultado de la operación por la pantalla.Órdenes de ensamblador vistas.
LEAx- calcula la dirección efectiva a la que hace referencia el operando y la almacena en x. x pueden ser X, Y, U o S
- Flags afectados: si x es X o Y, Z. Si no, ninguno.
Órdenes de la shell relacionadas.
ls- lista el contenido de un directorio
cd- cambia el directorio de trabajo
rm- borra un fichero
man- muestra la página de manual de una orden
cat- muestra el contenido de un fichero
echo $?- muestra el código devuelto por el último programa ejecutado