Inclusión de ficheros fuente
Se puede, en un punto cualquiera, incluir otro fichero que funcionará tal y como si lo hubiéramos tecleado en dicho punto. La orden es`include. Así, si
queremos incluir el fichero SumadorAuxiliar.v,
tecleamos:
`include "SumadorAuxiliar.v"
Ejercicio
El fichero74181.v contiene el
código Verilog
del ALU 74181 vista en teoría. Podéis encontrar el fichero
original en la página web del profesor
John P. Hayes,
de la Universidad de Michigan
(http://www.eecs.umich.edu/~jhayes/iscas.restore/74181.html).
Escríbase un
fichero Verilog con un módulo que realice las siguientes
operaciones usando dicha ALU:
- 7+4
- 2+6+1
- 01102 AND 10102
- 01102 XOR 10102
- 01102 OR NOT (10102 XNOR 01112) (2 operaciones)
- 2*7
- 3*5+1 (2 operaciones)
En el caso de operaciones múltiples, se deben usar registros para almacenar los valores intermedios. Recordemos el esquema y la tabla de operaciones de este circuito integrado:
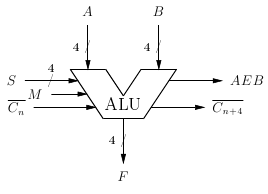

module Circuit74181 (S, A, B, M, CNb, F, X, Y, CN4b, AEB);os daréis cuenta de que las líneas de acarreo negadas son
CNb y CN4b, respectivamente. Las
líneas X e Y las podéis
dejar sin conectar.
Órdenes de la shell relacionadas.
ls- lista el contenido de un directorio
cd- cambia el directorio de trabajo
rm- borra un fichero
man- muestra la página de manual de una orden
cat- muestra el contenido de un fichero